29.1一维插值¶
Octave支持几种一维插值方法,大多数方法将在本节中介绍。多项式插值和散乱数据的插值描述其他方法。
- :
yi =interp1(x, y, xi)¶ - :
yi =interp1(y, xi)¶ - :
yi =interp1(…, method)¶ - :
yi =interp1(…, extrap)¶ - :
yi =interp1(…, "left")¶ - :
yi =interp1(…, "right")¶ - :
pp =interp1(…, "pp")¶ -
一维插值。
插入输入数据以确定的值易在点上xi如果没有指定,x被视为的指数y(
1:长度(y)). 如果y是矩阵或N维射线,对的每列执行插值y.插值方法是其中之一:
最近的-
返回最近的邻居。
前一个-
返回上一个邻居。
下一个-
返回下一个邻居。
-
线性的默认 -
最近邻居的线性插值。
pchip-
分段三次Hermite插值多项式——一阶导数光滑的保形插值。
立方体的-
三次插值(与
pchip). 样条曲线三次样条插值——平滑贯穿曲线的一阶导数和二阶导数。
将“*”添加到上述任何方法的开头
interp1假设x均匀间隔,且仅x1.和x2.被引用。这通常更快,而且永远不会更慢。默认方法为线性的.如果外推是字符串
外推,然后使用当前方法如果外推为anumber,则用该数字替换端点之外的值。当未指定时,外推默认为NA.如果字符串参数
pp则xi不应提供,并且interp1返回一个分段多项式对象。此对象以后可以与一起使用ppval以评估插值。有一个等价物,这样ppval(interp1(x,y, 方法,.pp), xi)==interp1(x,y, xi, 方法,外推)中的重复点x指定不连续的插入剂。最多可以有2个具有相同值的连续点。如果x正在增加,默认的不连续插入点是右连续的。如果x正在减少,默认的间断插入保持连续。插入装置的连续性条件可以通过使用参数来指定
左边或正确的以分别选择左连续插入物或右连续插入物。不连续插值只允许用于最近的和线性的方法;在所有其他情况下x-值必须是唯一的。的使用示例
interp1是xf=[0:0.05:10];yf=sin(2*pi*xf/5);xp=[0:10];yp=sin(2*pi*xp/5);lin=interp1(xp,yp,xf);near=interp1(xp,yp,xf,“最近的”);pch=interp1(xp,yp,xf,“pchip”);spl=interp1(xp,yp,xf,“样条曲线”);plot(xf,yf,“r”,xf,near,“g”,xf,lin,“b”,xf,pch,“c”,xf,spl,“m”,xp,yp,“r*”);图例(“原始”、“最近”、“线性”、“pchip”、“样条曲线”);
各种插值方法之间有一些重要的区别。这个样条曲线方法强制插值的一阶导数和二阶导数都具有连续导数,而其他方法则没有。这意味着的结果样条曲线方法通常更平滑。如果要插值的函数实际上是光滑的,那么样条曲线会取得优异成绩。然而,如果要评估的函数在某种程度上是不连续的,那么pchip插值可能会给出更好的结果。
这可以通过代码来证明
t=-2:2;dt=1;ti=-2:0.025:2;dti=0.025;y=符号(t);ys=interp1(t,y,ti,“样条曲线”);yp=interp1(t,y,ti,“pchip”);ddys=diff(diff(ys)/dti)。/dti;ddyp=diff(diff(yp)/dti)。/dti;图(1);绘图(ti,ys,“r-”,ti,yp,“g-”);图例(“样条曲线”、“pchip”,4);图2:绘图(ti,ddys,“r+”,ti,ddyp,“g*”);图例(“样条曲线”、“pchip”);
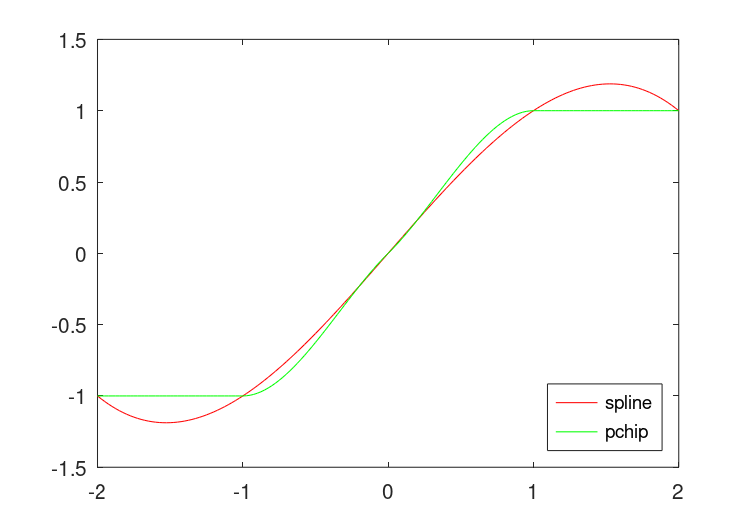
图29.1:的比较pchip和样条曲线astep函数的插值方法
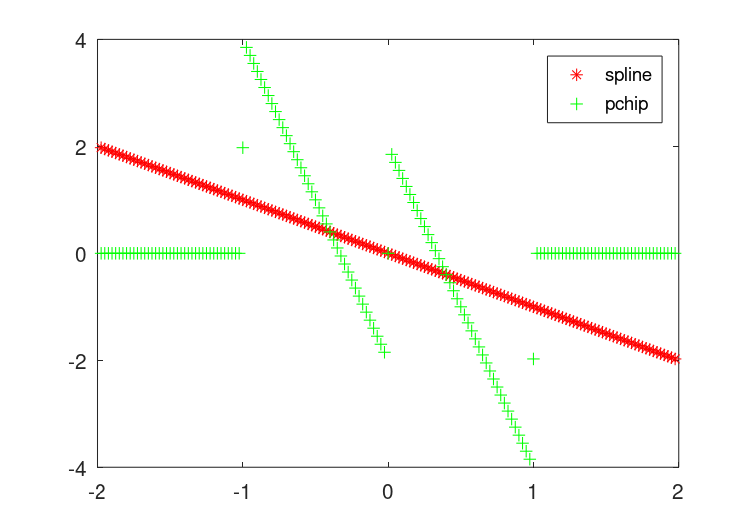
图29.2:的二阶导数的比较pchip和样条曲线阶跃函数的插值方法
傅立叶插值是一种重采样技术,将信号转换到频域,用零填充,然后再转换到时域。
- :
y =interpft(x, n)¶ - :
y =interpft(x, n, dim)¶ -
傅立叶插值。
如果x是向量,那么x使用重新采样n点。中的数据x假定是等距的。如果x是矩阵或N维数组,对的每列执行插值x.
如果dim指定,然后沿尺寸插入dim.
interft假设插值函数是周期性的,并对插值的端点进行假设。详见: interp1.
傅立叶插值有两个显著的局限性。首先,假设函数信号是周期性的,因此非周期性信号在边缘处表现不佳。其次,信号及其插值都需要在等空间点进行采样。的使用示例interft是
t=0:0.3:pi;dt=t(2)-t(1);n=长度(t);k=100;ti=t(1)+[0:k-1]*dt*n/k;y=sin(4*t+0.3).*cos(3*t-0.1);yp=sin(4*ti+0.3).*cos(3*ti-0.1);绘图(ti,yp,“g”,ti,interp1(t,y,ti,“样条曲线”),“b”。。。ti,interft(y,k),“c”,t,y,“r+”);图例(“sin(4t+0.3)cos(3t-0.1)”、“样条曲线”、“interft”、“data”);
这证明了傅立叶插值对非周期函数的不良行为,如中所示图29.3.
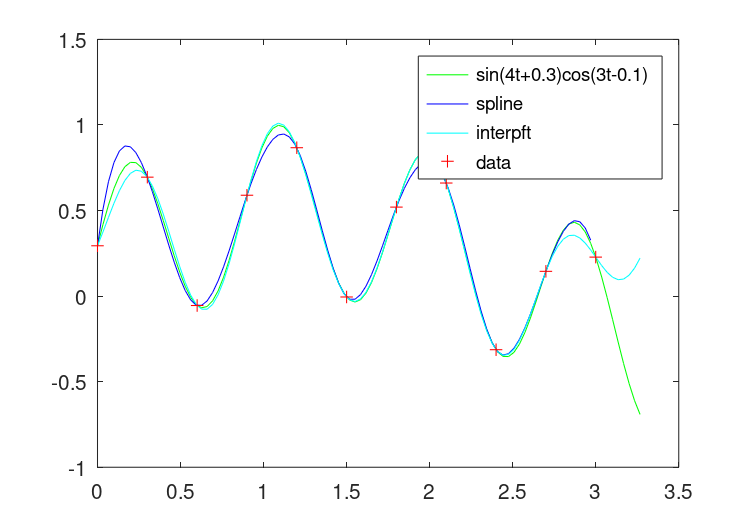
图29.3:的比较interp1和interft对于非周期性数据
此外,支持函数样条曲线和查找的基础interp1函数可以直接调用。
- :
pp =spline(x, y)¶ - :
yi =spline(x, y, xi)¶ -
返回点的三次样条插值x和y.
当使用两个参数调用时,返回分段多项式pp可以与一起使用
ppval以在特定点处多项式求值。当用第三输入自变量调用时,
样条曲线计算点处的样条曲线xi.第三种呼叫形式样条曲线(x, y, xi)相当于ppval(样条曲线(x, y), xi).变量x必须是长度的向量n.
y可以是向量或数组。如果y是一个向量,它的长度必须为n或
n2.。如果的长度y是n,然后不打结使用结束条件。如果的长度y是n2.,然后是向量的第一个值和最后一个值y是三次样条曲线在端点处的一阶导数的值。如果y是一个数组,那么的大小y必须具有表单
[s1, s2, …, sk, n]或[s1, s2, …, sk, n2.。数组内部被重塑为矩阵,其中前导尺寸从s1 * s2* … * sk然后将该矩阵的每一行分别处理。请注意,这恰好与相反interp1但已经结束了MATLAB兼容性。